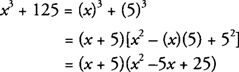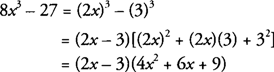Types of Factoring

• Difference of two squares
  • a²- b² = (a + b)(a - b)
  • (a-5)(a+5)
  • (x-10)(x-10)
  • (y-18)(y+18)
• Trinomial perfect squares  
•           x² + 6x + 9 = (x + 3)²
  •   x² − 4x + 4 = (x − 2)²
          x² + 10x + 25 = (x + 5)²
• Sum of two cubes
  • a³ + b³
    • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change

Example 1: Factor x³ + 125.


Example 2: Factor 8 x³ − 27.


Example 3: Factor 2 x³ + 128 y³.
First find the GFC. GFC = 2

• Sum of two cubes
  • a³ - b³ 
    • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change 
    •  
      x3 − 27= (x − 3)(x2 + 3x+ 9)  
    
    125 − x3=(5 − x)(25 + 5x + x2)
  • 
    1 − a3=(1 − a)(1 + a+ a2)
    
• Binomial expansion
  • (a + b)³ = Use the pattern
  • (a + b)⁴ = Use the pattern
  (5x - y)³ = 125x ³ -75x ² y + 15xy ² - y ³.

  (2x + 3y)4 =16x 4 +96x 3 y + 216x 2 y 2 +216xy 3 +81y 4

Quadratic Functions : Circles, Parabola, Elipse, Hyperbola

 Standard form of a Quadratic: ax² + bx + cy² + dy+e=0

If you have an equation like 7x² + 7y²=49 The equation is a circle, because a=c
http://www.webmath.com/cgi-bin/grapher.cgi?answer=y&cgiCall=grapher&getPost=get&param0=3&param1=-&param2=&param3=&param4=-&param5=&param6=&param7=-&param8=&param9=-&param10=&param11=&ymax=10&xmin=-10&xmax=10&ymin=-10&to_plot=circle

If a or c equals 0, the equation is a parabola ( ex: 7x² + 6y= 9)

If a or c have different signs the equation is a hyperbola ( for example: 2x² - 2y²= 8)

If you have an equation like 3x² + 4y²= 24 the equations is an ellipse, because a is not equal to c and the signs are the same


(x-h)² +(y-k)² =r ²  Standard form of a circle

Circle Formula      
 C=πr²                                                     Radius= diameter/2
 A=πr²                                                    Diameter=2r
What is a trinomial perfect square?
(a+b)²

Multiplying Matrices

To determine whether or not matrices can be multiplied you first have to write a dimensions statement.

Example of a dimensions statement:
[ 8 7 ]  [ 4 ]
[ 5  2 ]  [ 1 ]

Dimensions statement:
2 X 2 times 2 X 1



These matrices can be multiplied, so you would multiply row by column.
 Get the sum of the products.
The numbers in yellow tell you that you can multiply the matrices.
The numbers in green tell you the size of the final matrix.

Dimensions of Matrix

http://4.bp.blogspot.com/_12XEmpoNZy0/TI7NcHNjOmI/AAAAAAAAQOs/0vHIXoK_RbQ/s320/2x2_square.jpg

Thia ia a 2*2 MARIX

http://coachillclass-algii.blogspot.com/

1,3

http://1.bp.blogspot.com/_12XEmpoNZy0/TI7NfpdSY3I/AAAAAAAAQPE/ClM9fIJ6vY4/s320/3x3_square.jpg

1,3

http://1.bp.blogspot.com/_12XEmpoNZy0/TI7NfpdSY3I/AAAAAAAAQPE/ClM9fIJ6vY4/s1600/3x3_square.jpg

3,3

http://1.bp.blogspot.com/_12XEmpoNZy0/TI7NdQLPGTI/AAAAAAAAQO0/fNm6S5sgjV8/s1600/3x2.jpg.

3,2

http://1.bp.blogspot.com/_12XEmpoNZy0/TI7Neok2hoI/AAAAAAAAQO8/712PtJy-_4E/s1600/3x3_indentity.jpg

3,3

Error Analysis

http://2.bp.blogspot.com/_y62bUPRm_F8/TIWKIbktdsI/AAAAAAAAABE/TemCsmLq4cw/s1600/Page_4_Problem_9.jpg

Value of x is going up by 5 and the slope should be 10/5 or 2 not 10/1. Inserting the points, the final equation will be solved.  Y is not equal to 9+10x in the chart

http://1.bp.blogspot.com/_y62bUPRm_F8/TIWOx17uW_I/AAAAAAAAABM/Ukvh50eIPIA/s1600/Page_8_Problem_16.jpg

To have a point it must try to solve both equations. So (1,2) only solves the first one and not the second one

http://3.bp.blogspot.com/_y62bUPRm_F8/TIWPgyUgP7I/AAAAAAAAABU/-9Y0qel_LnM/s1600/Page_19_Problem_22_and_23.  

 20)shading is correct
  should be dotted line and not solid .
 #21 the solid line is correct, but the shading should be below the line, not above it.

http://4.bp.blogspot.com/_y62bUPRm_F8/TIWQyeLDOYI/AAAAAAAAABc/9X9WU4CNiug/s1600/Page_21_Problem_20_and_21.jpg

Graphing y=a|x-h|+k

y = a|x - h| + k

Although most books won't call the point (h,k) the vertex (as in quadratics) but it will either be a maximum or minimum value for the absolute value function.

If a > 0 , then (h,k) is the lowest point of the graph.  (opens upward)

If a < 0 , then (h,k) is the highest point of the graph.  (opens downward)

Types of Systems

Case 1	Case	Case 3

Independent system: one solution point	Case 2	Case 3

Independent system: one solution and one intersection point	Inconsistent system: no solution and no intersection point	Case 3

Independent  and consistent system: one solution and one intersection point	Inconsistent system: no solution and no intersection point	Dependent system: the solution is the whole line